

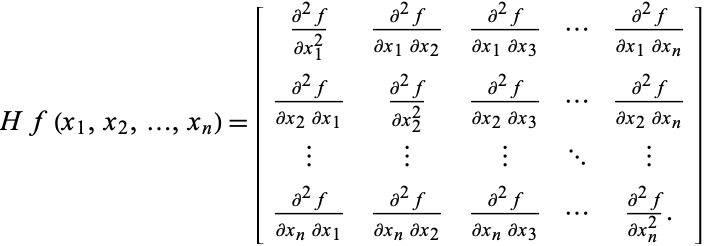
For example, suppose you wanted to find out how far a ball travels when thrown at an angle of 45 with an initial velocity of 50 meters per second. Some useful decomposition methods include QR, LU and Cholesky decomposition. If you don’t, WolframAlpha will produce a calculator in which you can dynamically change the values you did not specify. The determinant of the product of matrices is equal to the product of determinants of those matrices, so it may be beneficial to decompose a matrix into simpler matrices, calculate the individual determinants, then multiply the results. For a 2-by-2 matrix, the determinant is calculated by subtracting the reverse diagonal from the main diagonal, which is known as the Leibniz formula. Some matrices, such as diagonal or triangular matrices, can have their determinants computed by taking the product of the elements on the main diagonal. There are many methods used for computing the determinant. Geometrically, the determinant represents the signed area of the parallelogram formed by the column vectors taken as Cartesian coordinates. A system of linear equations can be solved by creating a matrix out of the coefficients and taking the determinant this method is called Cramer's rule, and can only be used when the determinant is not equal to 0. A determinant of 0 implies that the matrix is singular, and thus not invertible. The value of the determinant has many implications for the matrix. Knowledgebase about determinants A determinant is a property of a square matrix.
#Wolframalpha vector calculator generator#
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator find the determinant of the matrix ((a, 3), (5, -7)).To enter a matrix, separate elements with commas and rows with curly braces, brackets or parentheses.
Use plain English or common mathematical syntax to enter your queries. It can also calculate matrix products, rank, nullity, row reduction, diagonalization, eigenvalues, eigenvectors and much more. WolframAlpha can convert vectors to spherical or polar coordinate systems and can compute properties of vectors, such as the vector length or normalization. Wolfram|Alpha is the perfect resource to use for computing determinants of matrices. So whether your studies are in algebra, calculus, or physics, Wolfram|Alpha can be your resource for learning about vectors.More than just an online determinant calculator Wolfram|Alpha can even help you add and subtract two vectors using the tip-to-tail method. The radius gives you the magnitude of your vector, while the angles specify its direction. If you want to find both the magnitude and direction, you can represent the vector in polar or spherical coordinates. You can query Wolfram|Alpha for the vector’s length to find its magnitude:Īnd to find the direction, you can ask for the angles between the vector and the coordinate axes: Suppose you know only the point in R^n corresponding to your vector and you want to know its magnitude and direction. Wolfram|Alpha can now plot vectors with this arrow representation in 2D and 3D and return many other properties of the vector. The direction of the arrow matches the direction of the vector, while the length represents the magnitude of the vector. A vector is commonly defined as a quantity with both magnitude and direction and is often represented as an arrow. DiagonalMatrix list, k, n pads with zeros to create an n× n matrix. DiagonalMatrix list, k gives a matrix with the elements of list on the k diagonal. For example:Īnd in fact, Wolfram|Alpha can give lots of information on vectors. DiagonalMatrix list gives a matrix with the elements of list on the leading diagonal, and zero elsewhere. What do you get when you cross a mountain climber with a mosquito? Nothing-you can’t cross a scalar with a vector!īut what do you get when you cross two vectors? Wolfram|Alpha can tell you.


 0 kommentar(er)
0 kommentar(er)
